今回はモンテカルロ法をpythonで実装したので、紹介したいと思います。
モンテカルロ法とはシミュレーションや数値計算を乱数を用いて行う手法の総称です(Wikipedia)
今回はこのモンテカルロ法を用いてN次元単位超級の体積を求めていこうと思います。
半径\(r\)の\(n\)次元超級の体積は
$$V_n(r) = \frac{π^\frac{n}{2}}{Γ(\frac{n}{2}+1)}$$
で表されます。
こちらを近似するモンテカルロシミュレーションを実装しました。
import math
import numpy as np
import matplotlib.pyplot as plt
def V(n):
return math.pi**(n/2.0) / math.gamma(n/2.0+1.0)
def count_point(N, n):
x = []
count = 0
for i inrange(n):
x.append(np.random.uniform(-1.0, 1.0, N))
for i inrange(N):
r = 0.0
for j inrange(n):
r += x[j][i]**2.0
if r <1.0:
count += 1
return count
def main():
tv = []
mc = []
N = 100000#サンプル数
for n inrange(1,21):
c = count_point(N, n)
tv.append(V(n))
mc.append(2.0**n * float(c) / float(N))
print(n, 'Dim')
print('Theoretical Value:', V(n))
print('Monte Carlo :', 2.0**n *float(c) /float(N))
x = np.arange(1, 21, 1)
plt.plot(x, tv)
plt.plot(x, mc)
plt.xlabel('dimension')
plt.ylabel('Volume')
plt.title("N="+str(N))
plt.grid(True)
plt.show()
if __name__ == '__main__':
main()

N=1000での結果。ばらつきおおめ。
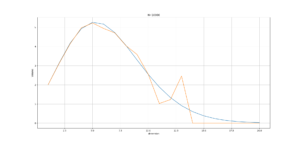
N=10000での結果。ばらつきがだいぶ減りました。

N=100000での結果。いい感じです。
モンテカルロ法で精度を上げるためには計算時間がより必要になっていきます。
合わせて読みたいpythonの記事はこちら
Sponsored Link
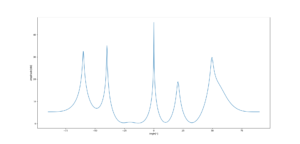
Pingback: pythonでMUSIC法
Pingback: pythonでMUSIC法を実装してみる