今回はpythonでインパルス応答を測定するためのプログラムを説明します。
まず、簡単にインパルス応答とはインパルス(時間的に継続時間が非常に短い信号)をシステムに入力した場合の出力を測定することです。
流れとしては...

インパルス信号をシステム(部屋などが一般的だが何でもよい)に入力します。
その出力がインパルス応答になります。
インパルス応答が取れると何がいいの?ということですが、
一つにはインパルス応答が分かっているシステムに、任意の入力信号を入力したときの出力信号が分かります。極端に言えば、あるシステムにコンサートのような臨場感ある音場を再現したいときにどのような音源を再生すればよいかなどが分かります。
他にもインパルス応答は有用な性質がたくさんあります。そこらへんはまた解説できればします。
で、そのインパルス応答を実際に測定するには単にパルスを入力して、システムの出力を得ればいいというわけではないのです。(SN比のため)
そのために様々な手法が提案されています。
代表的なものを紹介すると...
相互相関法・・・ホワイトノイズの自己相関関数がインパルスであることを利用して、入力信号の相互相関関数からインパルス応答を求める
クロススペクトル法・・・相互相関関数とクロススペクトルがフーリエ変換対であることを利用して、クロススペクトルからインパルス応答を求める
MLS法・・・入力にM系列信号を用いることで相互相関関数を求めるのに高速アマダール変換が利用でき、非常に高速にインパルス応答が求められる
TSP法・・・時間伸長信号:TSP信号を用いて、逆フィルタである時間反転した逆TSP信号で畳み込むことでインパルス応答を求める。現在はSwept-Sine法と呼ぶ
ざっとこんな感じです。
で、今回は一番下のTSP法(以下、Swept-Sine法)をpythonで実装していきます。
まずSwept-Sine信号とは周波数領域で以下の式で定義されます。
\[ SS(k)=\left\{ \begin{array}{ll} exp(j\alpha k^2) &(0\leq k\leq N/2) \\ exp(-j\alpha (N-k)^2) &(N/2\leq k\leq N-1) \end{array} \right. \]
kが周波数です。つまり、位相情報が\(k^2\)の定数倍で変化しています。これがSwept-Sine信号の特徴です。僕もよくわかってませんが、この信号を上手いこと入力させて、出力を得ます。
その後、逆Swept-Sine信号と出力を畳み込んで逆フーリエ変換すればインパルス応答をゲットできます。
ここらへんの詳しい説明はこちらの資料(5.3節あたりから)にお任せします。
で、僕はこの資料を基に円状畳込み原理を用いたインパルス応答測定(5.3.2あたりをよく読んでください)のアルゴリズムをpythonで実装しました。
では早速コードです。以下をインポート
import numpy as np
import matplotlib.pyplot as plt
import scipy.fftpack as fft
import soundfile as sf
import mathまずSwept-Sine信号は以下の要領で作ります。
def Swept-Sine():
gain = 70
TSP = 16384#信号長
m_exp = 1
m = TSP // (2 ** m_exp) # (J=2m)実効長m=(3/4)N~(1/2)N程度
a = ((m * np.pi) * (2.0 / TSP) ** 2)#α=4mπ/N^2
ss_freqs = np.zeros(TSP, dtype=np.complex128)
ss_freqs[:(TSP // 2) + 1] = np.exp(-1j * a * (np.arange((TSP // 2) + 1) ** 2))#exp(jαk^2)
ss_freqs[(TSP // 2) + 1:] = np.conj(ss_freqs[1:(TSP // 2)][::-1])
# ifft and real
ss = np.real(fft.ifft(ss_freqs))#逆フーリエ変換で信号作成
# roll
ss = gain * np.roll(ss, TSP//2 - m)#信号をシフトさせる
return(ss)これでサンプリングレート\(f_s\)の1/2まで遷移する信号が作成できます。(保存時や再生時にサンプリングレートを指定する)
このssをwavで保存するか、呼び出すかして再生できるようにしておきます。
上記で作った信号ssを用いて、インパルス応答の測定のための準備をしていきます。まずは測定信号作成。小文字が時間領域、大文字が周波数領域であることを意識して読んでください。
"""測定信号作成"""
ss_rep = np.r_[np.tile(ss, 3), np.zeros(TSP)]
#ssを3個ならべて、最後に無音部分(ssの1周期分)を追加→この3が同期加算回数の回数で多いほどSN比は向上する次に逆フィルタ作成。周波数領域で複素共役をとるだけ。信号には戻さない。
inv_SS = np.conj(fft.fft(ss))#周波数領域で複素共役あとはss_repを再生して、録音しましょう。自由にやってもらっても構いませんが、信号長を厳密に切り出すには同時に録音と再生を行う必要があります。
オーディオインターフェースを用いて同時録音・再生を行う方法は以下の記事で解説しています。得た出力をoutputとします。イメージはこんな感じです。
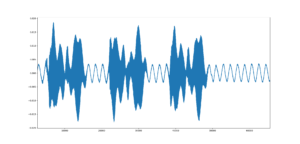
無音部分にも変な波が入っていますが、こちらを信号長で切り出して加算平均します。
"""出力の加算平均"""
start = 0
output_ave = np.zeros(TSP)
for i in range(3+1):並べた信号の数+1回
output_ave += output[start:start+TSP]#信号長の長さで頭から順に切り出す
start += TSP
output_ave /= 3#加算したものを割る(加算平均)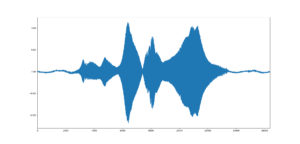
すると、確かにノイズの部分が抑えられている気がします。
後は、これと逆フィルタを周波数領域で掛け算(畳み込み)して、伝達関数を求めます。それを逆フーリエ変換すればよいだけです。
先ほど用意したinv_SSを使って...
"""伝達関数TF"""
TF = inv_SS*fft.fft(output_ave)
"""インパルス応答IR"""
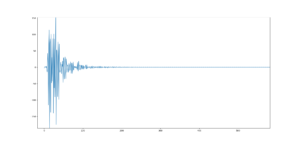
IR = fft.ifft(TF)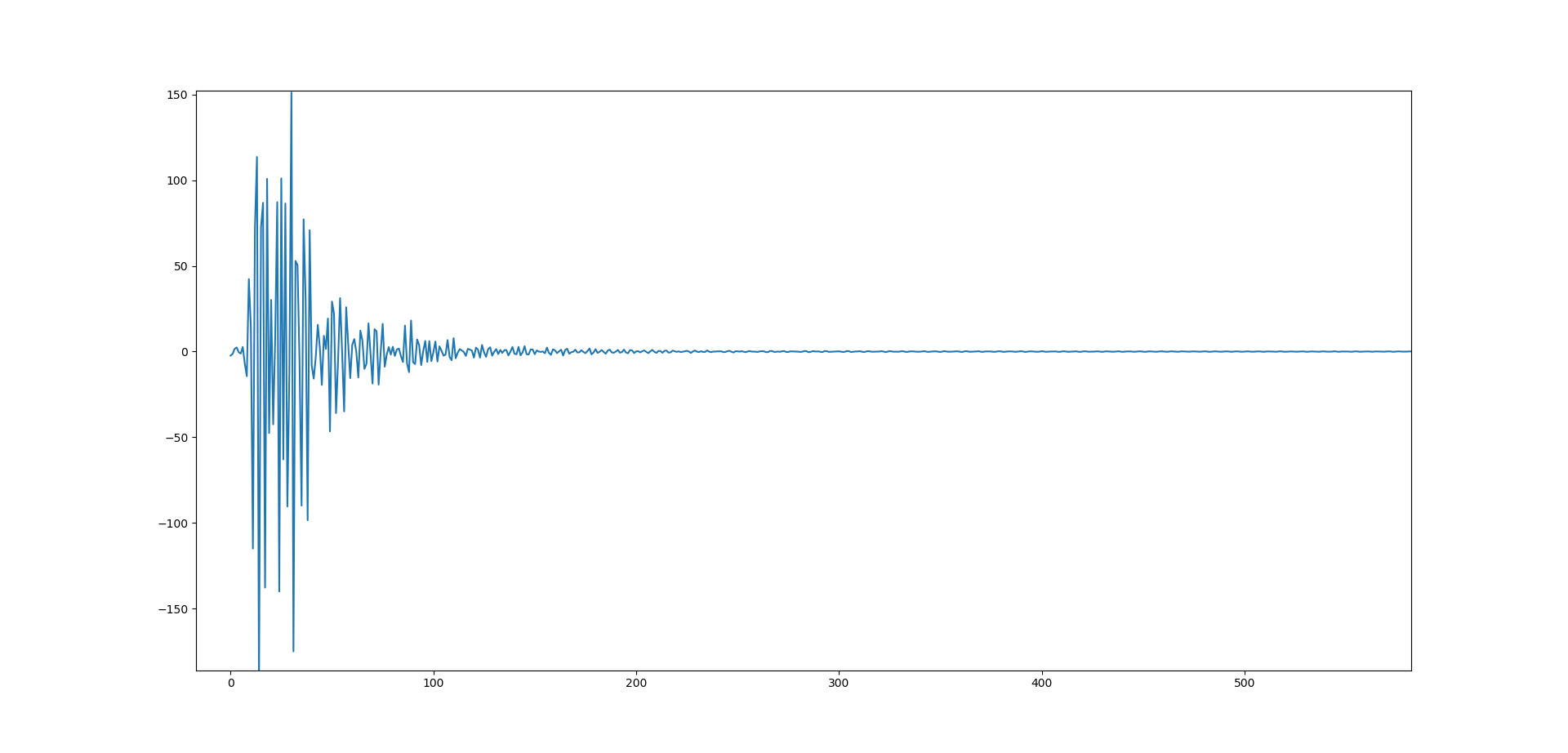
こんな感じでインパルス応答が出ます。
非常に簡単ですね。
注意点としてはインパルス応答の長さが信号長より短くないとこの方法は使えません。
信号長が長い場合は直線状畳み込みを用いた手法を使います。 Pythonでの実装方法は以下にまとめています。今後はMLS法も実装してみたいですね。
研究で外耳道内部の音を録音しているのですが、市販製品で録音するなら以下の商品で可能です。

Pingback: pythonでインパルス応答測定②[Swept-Sine法]
Pingback: pythonでチャープ(TSP/Sweep)信号を作成する