今回はチャープ信号をpythonで簡単に作成できるscipyのchirp関数を紹介します。

まずチャープ信号の説明からしていきます

チャープ信号とは？

チャープ信号とは時間とともに周波数が変化する信号のことを指しまして、周波数が増加する場合アップチャープ、減少する場合ダウンチャープと呼びます。また呼称としてスイープ(sweep)信号、TSP信号とも言います。

また線形関数的に変化する場合は線形チャープ、指数関数的に変化する場合は指数チャープなどと呼ばれ、用途によって使い分けます。

音響分野においてチャープ信号が使われるシーンはインパルス応答の測定などがあります。

インパルス応答についてはこちらの記事でPythonでの測定方法をまとめています。

簡単に説明しますと、すべての周波数帯の情報を含むインパルス信号を入力とすることで、ある伝達系の音響特性がすべてわかるという素晴らしい手法なんですが、単純なインパルス信号は出すのが難しくSN比が低いなど問題があります。

それを解決する方法としてチャープ信号が使われます。チャープ信号も周波数情報を時間領域に分散させた信号ですのでうまいことすればインパルス応答が取れます。
で、本題のpythonで実際に作ってみようという話です。

自作するとなると周波数領域で実現したいチャープの特性を表現して逆フーリエ変換するのが一般的です。

ではチャープ信号の作成方法を説明していきます。

Pythonでチャープ信号を実装する

今回はチャープ信号を手軽に生成できるpythonのscipyモジュールのchripメソッドで作成します！

使い方は簡単です。まず以下をインポートします。

from scipy.signal import chirp, spectrogram

で、この二行を書けば終わり。

t = np.linspace(0, 10, 5001) 
w = chirp(t, f0=6, f1=1, t1=10, method='linear')

二行目が本題のコードですが、引数が５つありますね。上から

t:波形の振幅値を割り振る時刻を格納する配列。今回は0~10秒を5001個に分割した時間分解能。

f0:最初の周波数。t[0]の周波数

f1:最後の周波数

t1:f1の周波数になるときの時刻

method:信号の種類(線形、二次、対数、双曲線)がある

簡単ですね。ではプロットもしていきます。

import matplotlib.pyplot as plt

plt.plot(t, w)
plt.title("Linear Chirp, f(0)=6, f(10)=1") 
plt.xlabel('t (sec)') 
plt.show()

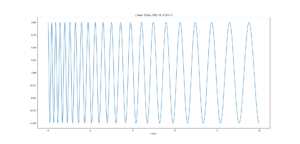
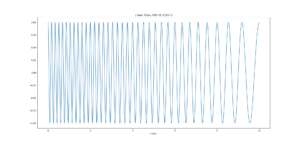
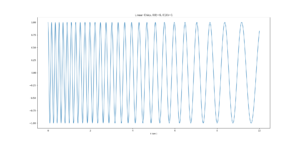
上から順に線形、二次、指数、双曲線関数で同じ時間、周波数をアップチャープさせました。

みにくいと思いますが若干変化が違いますね。

methodの計算式はドキュメントにあるので参考にしてください。

これで簡単に好きなチャープ信号が作れます。

pythonで音声処理をするなら、以下の本が入りやすくておすすめです。

Pythonで学ぶ実践画像・音声処理入門［伊藤克亘］

<br />