今回はpythonにて3dのプロットを行いたいと思います。
使うのはmpl_toolkits.mplot3dのAxes3Dというメソッドです。
表面を滑らかにプロットするplot_surfaceというのでプロットしたいと思います。
まずは簡単な例
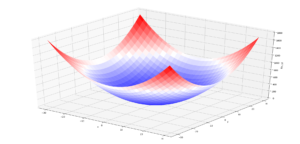
$$z=x^2+y^2$$
をプロットしてみましょう。
必要なものをインポート
import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D import numpy as np
次に\(z\)を返すメソッド
def func1(x,y): return x**2+y**2
後はメインでデータの準備とプロット処理
if __name__ == '__main__':
x = np.arange(-30,30,1)
y = np.arange(-30,30,1)
X, Y = np.meshgrid(x, y)
Z = func1(X,Y)
fig = plt.figure()
ax = Axes3D(fig)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("f(x, y)")
ax.plot_surface(X, Y, Z,cmap='bwr', linewidth=0)
plt.show()
これでこんな感じのグラフがぐりぐりできると思います。
オンラインで3dグラフを共有する方法もあるそうなので、また紹介します。
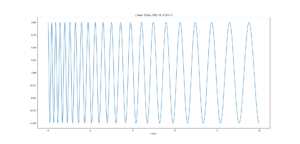
では次は音声の振幅スペクトルをプロットしてみます。
importに以下を追加
from scipy.signal import chirp, spectrogram from matplotlib import cm
今回はスイープ信号を窓をずらしながらフーリエ変換して、その変化を見てみます。
スイープ信号をpythonで作成する方法は以下の記事で解説しています。
メインに以下を追加しましょう。
N = 8192
fs = 48000#サンプリング周波数
t = np.linspace(0, 10, fs*10)
w = chirp(t, f0=0, f1=20000, t1=10, method='linear')#スイープ信号の生成
t = np.arange(0, N/fs, 1/fs) # 時間軸
freq = np.linspace(0, fs/2, int(N/2)-1) # 周波数軸
move = int(N)#移動量
x = np.arange(0,int((len(w)-move)/move),1)#フーリエ変換の回数分の配列を用意する。
X, FREQ = np.meshgrid(x, freq)
start = 0
hamming = np.hamming(N)#ハミング窓を用意する
Z = np.empty(int(N/2)-1)
for i inrange(int((len(w)-move)/move)-1):
data = w[start:start+N]#波形の抽出
spec = np.fft.fft(data*hamming)#窓をかけてフーリエ変換
Z = np.vstack((Z, abs(spec[1:int(N/2)])))#Zに追加
start += move#移動量分スタートをずらす
"""以下はプロット処理"""
fig = plt.figure()
ax = Axes3D(fig)
ax.set_xlabel("x")
ax.set_ylabel("freq")
ax.set_zlabel("f(x, y)")
ax.plot_surface(X, FREQ, Z.T, cmap=cm.coolwarm,linewidth=0)
plt.show()

分かりにくいかもしれませんが、ピークが遷移しています。
これは単なるスペクトログラムの3d化ですので、あまり使えるかわからないですけど
見やすくて面白いと思います。
みなさんもぜひ色んなデータを見やすくしてみてください。
pythonのグラフ描画はmatplotlibとseabornが定番。
以下の書籍で詳しく解説されています。
Sponsored Link