本日はpythonでMUSCI法を実装しましたので紹介していきます。
僕も理解はあまりできておらずととにかく使ってみよう!ということで計算式を実装しました
まず簡単なMUSIC法の説明
MUSIC法:Multiple Signal Classifier algorithmの略
おしゃれな名前ですね。僕がMUSIC法について調べていた時にはalgorithmのalも取ってMUSICALなんて言ってる人もいました(笑)
基本的なアイデアはPisarenkoさんの1973年の論文らしいです。詳しい説明はこちらの文献を参考にしてください。
本来は高分解能な周波数推定の一手法として考え出されましたが、現在は
・信号到来方向推定←今回はコレ!
・電磁波デバイスの時間領域推定←謎
・高分解能レーダーイメージング←なんかすごそう
など様々な応用がなされております。
ではどのような計算で実現しているかというと、
センサから受ける信号というのはは雑音部分空間と信号部分空間というものに分かれます。
そして雑音部分空間の固有ベクトルは信号部分空間に直交するという性質があるそうです。その性質を上手く利用するべく色々計算が必要なんですね。
そこら辺の計算式は先ほどの文献を参考にしてください。
大事なことだけいいますと、今回の信号到来方向推定だとやってくる信号の数よりセンシングするデバイスの数が多くないといけません。
例えば二つの音源の到来方向を知りたいなら三つ以上のマイクアレイが必要です。
以下がMUSIC法のpythonコードになります
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
import pandas as pd
import numpy.linalg as LA # linalgモジュールはLAとしてimportするのが慣例。
import math
data = pd.read_csv("to.csvPath")#センサデータのパス
M = 10#センサアレイの数
n = 100#スナップショット数,つまり何個のデータセットを使うかということ
res = 1000#推定する周波数分解能 180/res°になる
data = data.ix[0:n, :]
X =[]#センサデータを格納する行列(n×Mになるようにする)
X = signal.hilbert(data.T)#Xはデータそのままではなくヒルベルト変換を行う
X = X.T#計算のため転置する
R = [[0 for i in range(M)] for j in range(M)]#Xの分散共分散行列R
"""Rのための計算(関数を使ってもよい)"""
for i in range(M):
for j in range(M):
R_ij = 0
for k in range(n):
R_ij += X[k,i]* np.conjugate(X[k,j])
R[i][j] = R_ij/n
W, V = LA.eig(R)#Rの固有値W,固有ベクトルV
E = V[:,5:]#固有値の小さい固有ベクトルから順番に音源の数だけ抜きとりEとする
e = np.e#ネイピア数
div = np.pi/res#分解能
start = -np.pi/2
music_spec = np.empty(res)#MUSICスペクトラグラム。到来方向のインデックスあたりにピークが立つ
"""計算部分"""
for x in range(res):
sin = math.sin(start)
a = np.empty(10, dtype= complex)
for i in range(10):
s = pow(e, (complex(0, -(i+1)*np.pi)*sin))
a[i] = s
a_el = a.reshape((1,10))
a_el = np.conjugate(a_el)
E_el = np.conjugate(E.T)
bunsi = np.dot(a_el, a)
b_1 = np.dot(a_el, E)
b_2 = np.dot(b_1, E_el)
bunbo = np.dot(b_2, a)
music_spec[x] = 10*(np.log10(bunsi.real/bunbo.real))
start += div
"""可視化処理"""
x_axis = np.linspace(-90,90,res)
plt.plot(x_axis, music_spec)
plt.xlabel("Angle[°]")
plt.ylabel("Amplitude[dB]")
plt.show()
そして5つの音源の到来方向推定の結果がこちらです。
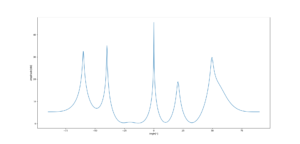
このようにきれいに5つの音源の到来方向を推定できています。
計算自体も簡単ですし、実装はそう難しくありません。
これからいろいろな研究で使われるようになると思いますので皆さんもぜひ使ってみてください。
音の信号処理はこの本がわかりやすいです。
合わせて読みたいpythonの記事はコチラ!!

大変参考になります。
不躾なお願いで申し訳ありませんが、
コード中のsignal.csvを公開していただけないでしょうか?
よしさん>
申し訳ございませんが、それは難しいです。
データに関してはご自身のものを用いていただくしかありません。
お力になれず、もうしわけありません。
とても勉強になります
コード中の”””計算部分”””についての質問なんですが、以下の
a = np.empty(10, dtype= complex)
for i in range(10):
a_el = a.reshape((1,10))
music_spec[x] = 10*(np.log10(bunsi.real/bunbo.real))
で使用されている10というのはセンサアレイ数が10だから10なのでしょうか?
そうですね。
Mに置き換えてもらった方が良いです。
よろしくお願いします。
Pingback: pythonでモンテカルロ法を実装する
MUSIC法を勉強中なのでとても参考になります。
csvファイルの中身についてお聞きしたいことがあります。
csvファイルの中身の1行には、10チャンネル分のデータが格納されているのでしょうか?
10チャンネル分のデータが格納された行がn行あるという認識であっていますでしょうか?
kinoさん
そうです。
参考になれば幸いです。
何度も申し訳ないです。
上のコードで変数dataのshapeは[100, M*サンプリングレート*秒数]ですか?
どうやって変数Xの2次元配列の形がn×Mになるのかがわかりません。
もしよろしければ教えていただきたいです。
行(変数n)がデータの数です
サンプリングレートなどによって実際の秒数は決まってきますが、今回はとりあえず1000サンプリングとってきたということです。(秒数は不明です)
列(変数M)はセンサの数ですので、何個のマイクで集音したかなどに依存します
参考になれば幸いです